Menghitung Volume Bangun Ruang

Menghitung Volume Bangun Ruang

1. Kubus

Kubus adalah bangun ruang tiga dimensi yang tersusun dari 6 bidang datar yang kongruen, keenam bidang kongruen pada kubus berbentuk persegi.

Keterangan: 

s = sisi kubus

Nama	Rumus
Volume (V)	V = s × s × s
	V = s³
Luas permukaan (L)	L = 6 × s × s
	L = 6 × s²

2. Balok

Balok adalah bangun ruang tiga dimensi yang tersusun oleh 3 pasang segi empat (persegi atau persegi panjang) dan paling sedikit mempunyai 1 pasangan sisi segi empat yang mempunyai bentuk yang berbeda.

Keterangan: 

t = tinggi 

p = panjang 

l = lebar

Nama	Rumus
Volume (V)	V = p × l × t
Luas Permukaan (L)	L = 2 × (p.l + p.t +l.t)

3. Prisma

Prisma adalah bangun ruang yang terdiri dari atap dan alas dengan bentuk segi-n yang kongruen beserta dipisahkan oleh sisi-sisi tegak berbentuk segi empat.

t = tinggi prisma

La = luas alas

Nama	Rumus
Volume (V)	V = Luas alas × t
tinggi (t) jika diketahui V	t = V ÷ Luas Alas
Luas Permukaan (L)	L = t × ( a1 + a2 + ... + an) + (2 × La)
	L = t × (Keliling Alas) + (2 × La)
∴ Luas Prisma Segi-3	L = t × ( a1 + a2 + a3) + (2 × La)
∴ Luas Prisma Segi-4	L = t × ( a1 + a2 + a3 + a4) + (2 × La)
∴ Luas Prisma Segi-5	L = t × ( a1 + a2 + a3 + a4 + a5) + (2 × La)
∴ Luas Prisma Segi-6	L = t × ( a1 + a2 + a3 + a4 + a5 + a6) + (2 × La)
Luas Alas (La)	Disesuaikan dengan bentuk prisma

4. Limas Segitiga

Limas segitiga adalah bangun ruang berjenis limas yang mempunyai sisi alas berbentuk segitiga. Secara umum, Limas adalah jenis bangun ruang yang mempunyai sisi alas berbentuk segi-n dan mengerucut ke satu titik sehingga terbentuk sisi-sisi tegak berbentuk segitiga.

Keterangan:

t = tinggi limas (PO)

as = alas segitiga (AB)

ts = tinggi segitiga alas (DC)

t1, t2, t3 = tinggi masing-masing bidang tegak

a1, a2, a3 = alas masing-masing bidang tegak

Nama	Rumus
Volume (V)	V = ⅓ × La × t
	V = ⅓ × (½ × as × ts) × t
Luas Permukaan (L)	L = L alas + L ΔI + L ΔII + L ΔIII

5. Limas Segiempat

Limas segi empat adalah bangun ruang sejenis limas yang mempunyai alas segi empat (persegi, persegi panjang, belah ketupat, layang-layang, jajar genjang atau trapesium).

Nama	Rumus
Volume (V)	V = ⅓ × L alas × t
Luas Permukaan (L)	L = L alas + L ΔI + L ΔII + L ΔIII + L ΔIV
Tinggi	t = (3 × V) ÷ L alas

Luas Alas Limas Segi Empat

Jenis Alas	Luas Alas (La)
Alas Persegi	La = s × s
Alas Persegi Panjang	La = p × l
Alas Jajar Genjang	La = a × t
Alas Trapesium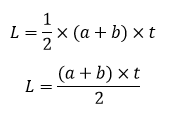
Alas Belah Ketupat	La = ½ × d1 × d2
Alas Layang-Layang	La = ½ × d1 × d2

6. Tabung

Tabung adalah bangun ruang yang tersusun oleh 3 buah sisi yaitu 2 buah lingkaran yang mempunyai ukuran yang sama dan 1 segiempat yang mengelilingi kedua lingkaran tersebut.

Keterangan: 

t = tinggi 

r = jari-jari (r)

d = diameter (d)

π = 22/7 untuk jari-jari kelipatan 7 dan 3,14 untuk jari-jari bukan kelipatan 7

Nama	Rumus
Volume (V)	V = π × r × r × t
	V = π × r² × t
Luas Permukaan (L)	L = 2 × π × r × (r + t)
Luas Selimut (Ls)	Ls = 2 × π × r × t
	Ls = π × d × t
Luas alas (La)	La = π × r × r

7. Kerucut

Kerucut adalah bangun ruang yang memiliki 2 sisi yaitu sebuah lingkaran dan sebuah bidang lengkung.

Keterangan:

t = tinggi

r = jari-jari

s = panjang garis pelukis (apotema), merupakan garis yang menghubungkan titik puncak dengan titik keliling alas kerucut.

Nilai s dapat dihitung menggunakan rumus Pythagoras. 

π = 22/7 untuk jari-jari (r) kelipatan 7 dan 3,14 untuk jari-jari bukan kelipatan 7

Nama	Rumus
Volume (V)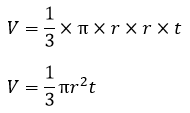
Luas permukaan (L)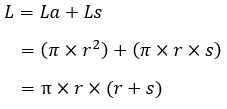
Luas alas (La)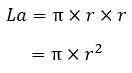

8. Bola

Bola adalah bangun ruang dengan bentuk bulat sempurna yang tersusun oleh tidak terhingga lingkaran yang mempunyai jari-jari dan pusat lingkaran yang sama.

r = jari-jari (r) 

d = diameter (d) 

π = 22/7 untuk jari-jari kelipatan 7 dan 3,14 untuk jari-jari bukan kelipatan 7

Nama	Rumus
Volume (V)	V = 4/3 × π × r³
Luas Permukaan (L)	L = 4 × π × r²

Materi selanjutnya, Contoh Soal Bangun Ruang... See U...